Download determinant form of `(x y)(y z)(z x)(x y z)` MP3 & MP4 You can download the song determinant form of `(x y)(y z)(z x)(x y z)` for free at MetroLagu. To see details of the determinant form of `(x y)(y z)(z x)(x y z)` song, click on the appropriate title, then the download link for determinant form of `(x y)(y z)(z x)(x y z)` is on the next page.

	Determinant form of `(x-y)(y-z)(z-x)` (Doubtnut) View
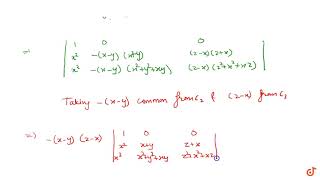	Determinant form of `(x-y)(y-z)(z-x)(xy+yz+zx)` (Doubtnut) View
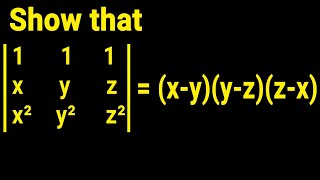	Show that the determinant is equal to (x-y)(y-z)(z-x) (IQ Initiative) View
	Determinant form of `(x-y)(y-z)(z-x)(x+y+z)` (Doubtnut) View
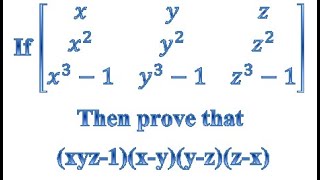	(xyz-1)(x-y)(y-z)(z-x) (Amit School) View
	Using properties of determinants, prove that `[[-yz, y^2+yz, z^2+yz], [x^2+xz, -xz, z^2+xy], [ (Doubtnut) View
	Find the values of x,yand z from the following equations [ 4 3 x 5 ] = [ y z 1 5 ] (Fountain of Mathematics) View
	`\|(0,xyz,x-z),(y-x,0,y-z),(z-x,z-y,0)\|` is equal to�� (Doubtnut) View
	Implicit Differentiation With Partial Derivatives Using The Implicit Function Theorem \| Calculus 3 (The Organic Chemistry Tutor) View
	By using properties of determinants. Show that: `\|xx^2y z y y^2z x z z^2x y\|=(x-y)(y-z)(z-x)(x y... (Doubtnut) View